تینا مزدکی_دانشمندان دانشگاه موناش استرالیا موفق شدهاند یکی از قدیمیترین مسائل هندسی را که به قرن هفدهم بازمیگردد، با استفاده از مفاهیم فیزیکی حل کنند. این دستاورد، گامی بزرگ در تعمیم قضیه دایرههای دکارت به شمار میرود.
قضیه دکارت که یکی از اصول مهم هندسه محسوب میشود، رابطهی میان چهار دایرهی مماس با یکدیگر را توصیف میکند. با این حال، تعمیم این رابطه به بیش از چهار دایره، قرنها ذهن ریاضیدانان را به خود مشغول کرده بود—تا اینکه پژوهشگران دانشگاه موناش راهحلی برای آن یافتند.
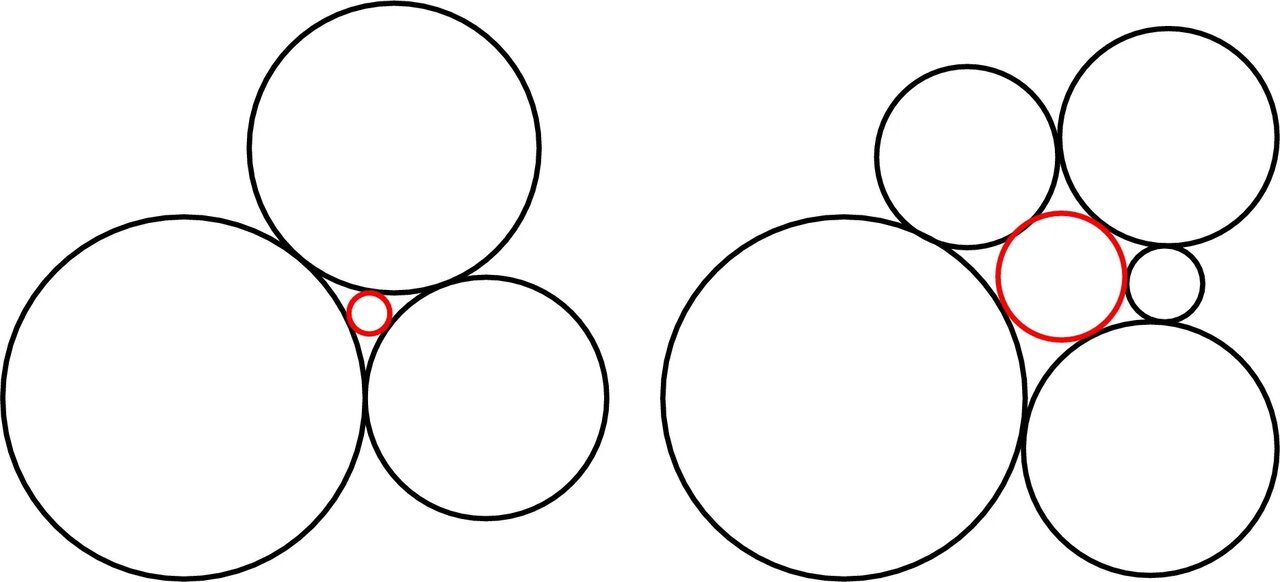
استادیار دنیل متیوز از دانشکده ریاضیات دانشگاه موناش، همراه با اوریون زیماریس، دانشجوی دکتری، موفق به کشف معادلهای شدند که الگوهای هندسی پیچیده موسوم به «n-گلها» (n-flowers) را توصیف میکند؛ ساختارهایی متشکل از چند دایرهی مماس که در نظریه بستهبندی دایرهها نقش بنیادی دارند.
به گفته این پژوهشگران، اگر انحنای دایرههای بیرونی (گلبرگها) مشخص باشد، میتوان انحنای دایرهی مرکزی را با دقت بالا محاسبه کرد. آنها برای دستیابی به این معادله از ابزاری استفاده کردند که معمولاً در مکانیک کوانتومی و نظریه نسبیت کاربرد دارد: اسپینورها.
از دکارت تا اسپینورها
متیوز در بیانیهای اعلام کرد:«دکارت در سال ۱۶۴۳ مسئلهای را برای پرنسس الیزابت مطرح کرد که تصور میکرد قادر به حل آن است. اما نتوانست. در نهایت، نسخهای سادهشده از آن مسئله تبدیل به قضیه کلاسیک دکارت شد.»
اگرچه تلاشهایی برای تعمیم این قضیه صورت گرفته بود، اما این نخستین بار است که معادلهای صریح برای هر تعداد دلخواه از دایرههای مماس ارائه میشود. زیماریس، که تحقیق دکتری او منجر به این کشف شد، توضیح داد که روش آنها از ابزارهای هندسی پیشرفته الهام گرفته از فیزیک استفاده میکرد: «ما از نسخهای از اسپینورها بهره بردیم که توسط راجر پنروز، برنده جایزه نوبل، و ولفگانگ ریدلر توسعه یافتهاند، اسپینورهایی که در نظریه نسبیت کاربرد دارند. جالب است که همان ساختارهای ریاضی که برای توصیف اسپین کوانتومی و نسبیت استفاده میشوند، اکنون میتوانند در درک بهتر ساختارهای دایرهای نیز نقش ایفا کنند.»
پاسخی نو به پرسشی کهن
این پژوهش تنها گامی مهم در ریاضیات محض نیست، بلکه گواهی است بر قدرت روزافزون گروه توپولوژی دانشگاه موناش که اکنون شامل ۹ دانشجوی دکتری است که پنج نفر از آنها زنان هستند. متیوز در پایان اظهار داشت: «این کشف، نمونهای هیجانانگیز از آن است که چگونه مسائل کلاسیک میتوانند پس از قرنها الهامبخش ریاضیات نوین باشند. فوقالعاده است که ببینیم پرسشی که دکارت در قرن هفدهم با آن دستوپنجه نرم میکرد، هنوز هم پاسخهای تازهای برای ارائه دارد.»
منبع: interestingengineering
۲۲۷۳۲۳

ارسال نظر شما
مجموع نظرات : 0 در انتظار بررسی : 0 انتشار یافته : 0